
1. Выяснить, принадлежит ли точка с координатами (x, y) кругу единичного радиуса с центром в начале координат.
2. Даны действительные числа x, y, z. Вывести на печать:
a). Максимальное из чисел x, y, z.
b). Минимальное из чисел x, y, z.
c). Максимальное и минимальное из чисел x, y, z.
3. Даны действительные числа x, y, z. Удвоить эти числа, если x≥y≥z, и заменить их абсолютными значениями, если условия не
выполняются.
4. Даны действительные числа x, y, z. Проверить, выполняется ли неравенства x≥y≥z, и напечатать результат проверки.
5. Даны действительные числа x, y. Вычислить z по одной из формул
и вывести на печать: 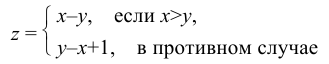
6. Даны два действительных числа. Заменить первое число нулем, если оно меньше или равно второму, и оставить числа без
изменения в противном случае.
7. Даны действительные числа x, y, z. Напечатать из них те, которые принадлежат интервалу [0 . . 4].
8. Даны положительные действительные числа x, y, z. Выяснить, существует ли треугольник с длинами сторон x, y, z, и напечатать соответствующее сообщение.
9. Даны два действительных числа. Возвести в квадрат те из них, значения которых неотрицательны.
10. Даны два различных действительных числа. Преобразовать:
a). Меньшее из чисел заменить из полусуммой, а большее из них заменить их удвоенным произведением.
b). Большее из чисел заменить из полусуммой, а меньшее из них заменить их удвоенным произведением.
11. Даны действительные числа x, y. Если x, y отрицательные, то каждое значение заменить их модулем, если отрицательно только одно из них, то оба значения увеличить на 1, в противном случае оставить без изменения.
12. Даны действительные числа x, y. Если x, y отрицательные, то каждое значение заменить их модулем, если отрицательное только одно из них, то оба уменьшить в 10 раз, в противном случае оставить без изменения.
13. Даны действительные числа x, y. Если x, y положительные, и оба значения не принадлежат отрезку [1,5 . . 3,2], то каждое значение увеличить в два раза, в противном случае уменьшить в два раза.
14. Если сумма трех различных действительных чисел x, y, z меньше единицы, то наименьшее из этих трех чисел заменить полусуммой двух других, в противном случае заменить большее из x, y полусуммой оставшихся значений.
15. Если сумма трех различных действительных чисел x, y, z больше единицы, то наибольшее из этих трех чисел заменить полусуммой двух других, в противном случае заменить меньшее из x, y полусуммой оставшихся значений.
16. Даны действительные числа a, b, c, d. Выяснить, можно ли прямоугольник со сторонами a, b уместить внутри прямоугольника со сторонами c, d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника. Выдать соответствующее сообщение.
17. Даны действительные числа a, b, c, d, e. Выяснить, пройдет ли кирпич с ребрами a, b, e в прямоугольное отверстие со сторонами c, d так, чтобы каждое из ребер было параллельно или перпендикулярно каждой из сторон отверстия. Выдать
соответствующее сообщение.
18. Дано действительное число x. Вычислить и напечатать значение
функции F(x) по формулам:
a) 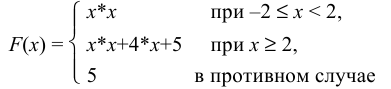
b) 
c) 
19. Заданы координаты двух точек. Определить:
a) Лежат ли они на одной окружности с центром в начале координат. Результат присвоить символьной переменной и вывести
ее на печать. Две точки лежат на одной окружности, если длины радиус-векторов, соединяющих эти точки с началом координат,
равны. Проверку на равенство вещественных чисел производить с точностью до 0,0001.
b) Принадлежат ли они кольцу с центром в начале координат с внешним радиусом 4 и внутренним радиусом 2,5.
20. Заданы площади круга и квадрата. Определить, поместится ли круг в квадрате. Квадрат поместится в круге, если его диагональ меньше или равна диаметру окружности.
21. Заданы площади круга и квадрата. Определить, поместится ли квадрат в круге. Круг поместится в квадрате, если его диаметр
меньше или равен стороне квадрата.
22. Даны результаты по бегу на дистанцию 100 метров трех спортсменов. Выбрать и напечатать лучший результат.
23. составить программу, реализующую эпизод сказки. Компьютер спрашивает, куда пойдет герой (налево, прямо или направо) и печатает, что его ожидает в каждом случае. Ответы ЭВМ хранить в символьных переменных. Тексты вопросов и ответов задать самостоятельно.
24. Составить программу, контролирующую знание закон Ома. Пользователь вводит закон Ома в символьную переменную.
Сравнить пользовательский ответ с правильным ответом, хранящимся в другой символьной переменной. Перед вводом
формулы напечатать указание, с использованием каких обозначений следует осуществить ввод.
























