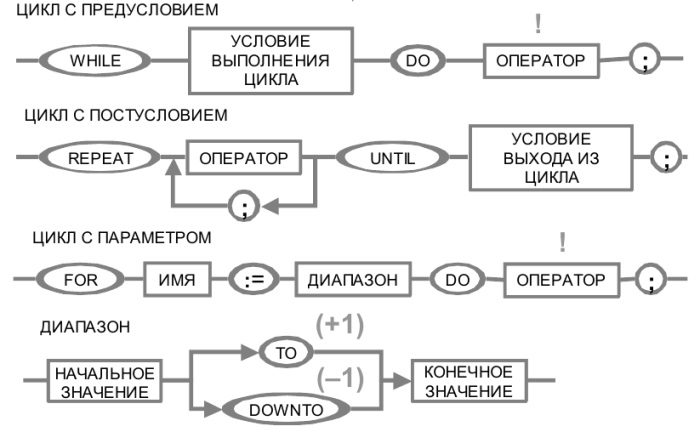
Вычислить сумму бесконечно сходящегося ряда. 

1) Вычислить и вывести на печать в виде таблицы все значения аргумента (x – положительное вещественное число) и функции при n = 1, 2, … , 40:
a). y = sin (nx )– cos(nx) ;
b). y = lg(nx)/x ;
c). y = (x+1)n.
2. Вычислить и запомнить в массиве значения функции (a, b, c – целые числа).
a). y = a*ex (b–cx )при изменении x от 0 до 2 с шагом 0,1;
b). y = sin(ax)– cos(bx) c при изменении x от значения –π до π с шагом 0,2.
3. Запомнить в массиве A положительные значения функции y при изменении x от 0 до 10 с шагом 0,1. Вывести на печать полученный массив A (a, b, c – вещественные числа):
a). y = –x3 + a*x2 + b*x + c;
b). y = (sin a(x )– cos b(x))/c
4. Запомнить в массиве A отрицательные значения функции y при изменении x от 0 до 10 с шагом 0,1. Вывести на печать полученный массив A (a, b, c – вещественные числа):
a). y = –x3 + a*x2 + b*x + c;
b). y = (sin(ax)– cos(bx))/c
5. Дано натуральное число n и вещественное число a. Вычислить и напечатать без использования операции возведения в степень:
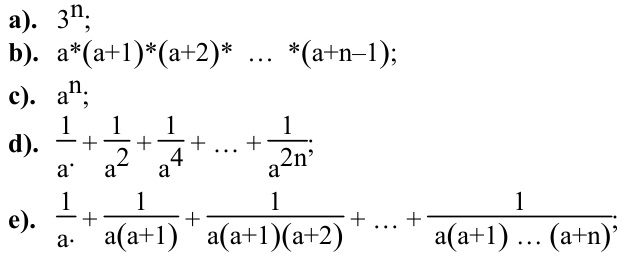
6. Дано действительное число a. Найти и напечатать:
a). Первое число из чисел 1, 1+1/2, 1+1/2+1/3, …, которое больше a;
b). Наименьшее целое число n, при котором 1+1/2+1/3+ … 1/n > a.
7. Напечатать таблицу перевода температуры из градусов по шкале Цельсия (°С) в градусы шкалы Фаренгейта (°F) для значений от 16 до 45 °C с шагом 0,5. перевод осуществлять по формуле F = 1,8*C+32.
8. Напечатать таблицу соответствия между весом в фунтах и весом в килограммах. Сопоставить значения от 1 до 20 фунтов с шагом в 1 фунт (1 фунт = 400 килограмм).
9. напечатать таблицу перевода расстояний в дюймах в сантиметры (1 дюйм = 2,54 сантиметра). Сопоставить значения от 1 до 10
дюймов с шагом 1 дюйм.
10. Составить и напечатать таблицу умножения для числа 12. таблица умножения для числа n – это результаты умножения 1*n, 2+n, …, n*n.
11. Начав тренировки, спортсмен пробежал в первый день 10 км. Каждый следующий день он увеличивал дневную норму на 10% от нормы предыдущего дня. Какой суммарный путь пробежал спортсмен за неделю?
12. В задаче №11 определить, через сколько дней спортсмен пробежит суммарный путь 100 км.
13. В задаче №11 определить, через сколько дней спортсмен будет пробегать в день больше 20 км.
14. Одноклеточная амеба каждые 3 часа делится на две клетки. Определить, сколько клеток будет через 3, 6, 9, … , 24 часа. Считать, что в начальный момент была одна клетка.
15. Вычислить сумму членов ряда с точностью до члена ряда, меньшего 0,0001. для определения текущего члена ряда
использовать рекуррентную формулу:
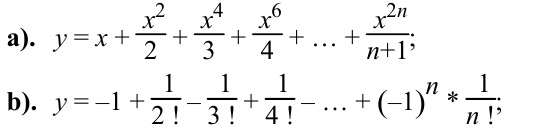
16. Дан расходящийся ряд x + (3x+1) + (5x+2) + (7x+3) + … Найти сумму элементов, абсолютные величины которых не превышают 500.
























